There’s a nice post by Ryou about the projections feature of Eric Niebler’s ranges that we’re going to get in C++20.

I’ll try to provide a more general look at what projections are – not only in the context of ranges. I recommend reading Ryou’s post before or after this one for completeness.

Tables have turned

Imagine the following – you have a collection of records where each record has several fields. One example of this can be a list of files where each file has a name, size and maybe something else.

Collections like these are often presented to the user as a table which can be sorted on an arbitrary column.

By default std::sort uses operator< to compare items in the collection while sorting which is not ideal for our current problem – we want to be able to sort on an arbitrary column.

The usual solution is to use a custom comparator function that compares just the field we want to sort on (I’m going to omit namespaces for the sake of readability, and I’m not going to write pairs of iterators – just the collection name as is customary with ranges):

sort(files, [] (const auto& left, const auto& right) {
                return left.name < right.name;
            });

There is a lot of boilerplate in this snippet for a really simple operation of sorting on a specific field.

Projections allow us to specify this in a much simpler way:

sort(files, less, &file_t::name);

What this does is quite simple. It uses less-than for comparison (less), just as we have with normal std::sort but it does not call the operator< of the file_t objects in order to compare the files while sorting. Instead, it only compares the strings stored in the name member variable of those files.

That is the point of a projection – instead of an algorithm testing the value itself, it tests some representation of that value – a projection. This representation can be anything – from a member variable, to some more complex transformation.

One step back

Let’s take one step back and investigate what a projection is.

Instead of sorting, we’re going to take a look at transform. The transform algorithm with an added projection would look like this:

transform(files, destination,
          [] (auto size) { return size / 1024; }, &file_t::size);

We’re transforming a collection of files with a &file_t::size projection. This means that the transform algorithm will invoke the provided lambda with the file sizes instead of file_t objects themselves.

The transformation on each file_t value in the files collection is performed in two steps:

• First, for a file f, extract f.size
• Second, divide the result of the previous step by 1024

This is nothing more than a function composition. One function gets a file and returns its size, and the second function gets a number and divides it by 1024.

If C++ had a mechanism for function composition, we would be able to achieve the same effect like so:

transform(files, destination,
    compose_fn(
        [] (auto size) { return size / 1024; },
        &file_t::size
    ));

Note: compose_fn can be easily implemented, we’ll leave it for some other time.

Moving on from transform to all_of. We might want to check that all files are non-empty:

all_of(files, [] (auto size) { return size > 0; }, &file_t::size);

Just like in the previous example, the all_of algorithm is not going to work directly on files, but only on their sizes. For each file, the size will be read and the provided predicate called on it.

And just like in the previous example, this can be achieved by simple function composition without any projections:

all_of(files,
    compose_fn(
        [] (auto size) { return size > 0; },
        &file_t::size
    ));

Almost composition

The question that arises is whether all projections can be replaced by ordinary function composition?

From the previous two examples, it looks like the answer to this question is “yes” – the function composition allows the algorithm to “look” at an arbitrary representation of a value just like the projections do. It doesn’t matter whether this representation function is passed in as a projection and then the algorithm passes on the projected value to the lambda, or if we compose that lambda with the representation function.

The things stop being this simple when an algorithm requires a function with more than one argument like sort or accumulate do.

With normal function composition, the first function we apply can have as many arguments as we want, but since it returns only a single value, the second function needs to be unary.

For example, we might want to have a function size_in which returns a file size in some unit like kB, KiB, MB, MiB, etc. This function would have two arguments – the file we want to get the size of and the unit. We could compose this function with the previously defined lambda which checks whether the file size is greater than zero.

sort needs this to be the other way round. It needs a function of two arguments where both arguments have to be projected. The representation (projection) function needs to be unary, and the resulting function needs to be binary.

Universal projections

So, we need a to compose the functions a bit differently. The representation function should be applied to all arguments of an n-ary function before it is called.

As usual, we’re going to create a function object that stores both the projection and the main function.

template <typename Function, typename Projection>
class projecting_fn {
public:
    projecting_fn(Function function, Projection projection)
        : m_function{std::move(function)}
        , m_projection{std::move(projection)}
    {
    }

    // :::

private:
    Function m_function;
    Projection m_projection;
};

The main part is the call operator. It needs to project all the passed arguments and then call the main function with the results:

template <typename... Args>
decltype(auto) operator() (Args&&... args) const
{
    return std::invoke(
               m_function,
               std::invoke(m_projection, FWD(args))...);
}

This is quite trivial – it calls m_projection for each of the arguments (variadic template parameter pack expansion) and then calls m_function with the results. And it is not only trivial to implement, but it is also trivial for the compiler to optimize.

Now, we can use projections even with old-school algorithms from STL and in all other places where we can pass in arbitrary function objects.

To continue with the files sorting example, the following code sorts a vector of files, and then prints the files to the standard output all uppercase like we’re in 90s DOS:

    std::sort(files.begin(), files.end(),
              projecting_fn { std::less{}, &file_t::name });

    std::copy_if(
              files.cbegin(), files.cend(),
              std::ostream_iterator<std::string>(std::cout, " "),
              projecting_fn {
                  string_to_upper,
                  &file_t::name
              });

Are we there yet?

So, we have created the projected_fn function object that we can use in the situations where all function arguments need to be projected.

This works for most STL algorithms, but it fails for the coolest (and most powerful) algorithm – std::accumulate. The std::accumulate algorithm expects a function of two arguments, just like std::sort does, but it only the second argument to that function comes from the input collection. The first argument is the previously calculated accumulator.

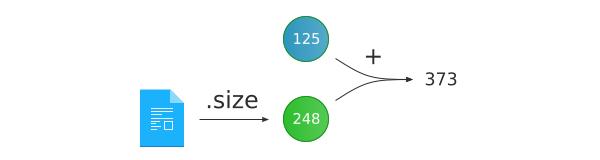
This means that, for accumulate, we must not project all arguments – but only the last one. While this seems easier to do than projecting all arguments, the implementation is a tad more involved.

Let’s first write a helper function that checks whether we are processing the last argument or not, and if we are, it applies m_projection to it:

template <
    size_t Total,
    size_t Current,
    typename Type
    >
decltype(auto) project_impl(Type&& arg) const
{
    if constexpr (Total == Current + 1) {
        return std::invoke(m_projection, std::forward<Type>(arg));
    } else {
        return std::forward<Type>(arg);
    }
}

Note two important template parameters Total – the total number of arguments; and Current – the index of the current argument. We perform the projection only on the last argument (when Total == Current + 1).

Now we can abuse std::tuple and std::index_sequence to provide us with argument indices so that we can call the project_impl function.

template <
    typename Tuple,
    std::size_t... Idx
    >
decltype(auto) call_operator_impl(Tuple&& args,
                                  std::index_sequence<Idx...>) const
{
    return std::invoke(
            m_function,
            project_impl
                <sizeof...(Idx), Idx>
                (std::get<Idx>(std::forward<Tuple>(args)))...);
}

The call_operator_impl function gets all arguments as a tuple and an index sequence to be used to access the items in that tuple. It calls the previously defined project_impl and passes it the total number of arguments (sizeof...(Idx)), the index of the current argument (Idx) and the value of the current argument.

The call operator just needs to call this function and nothing more:

template <typename... Args>
decltype(auto) operator() (Args&&... args) const
{
    return call_operator_impl(std::make_tuple(std::forward<Args>(args)...),
                              std::index_sequence_for<Args...>());
}

With this we are ready to use projections with the std::accumulate algorithm:

std::accumulate(files.cbegin(), files.cend(), 0,
    composed_fn {
        std::plus{},
        &file_t::size
    });

Epilogue

We will have projections in C++20 for ranges, but projections can be useful outside of the ranges library, and outside of the standard library. For those situations, we can roll up our own efficient implementations.

These even have some advantages compared to the built-in projections of the ranges library. The main benefit is that they are reusable.

Also (at least for me) the increased verbosity they bring actually serves a purpose – it better communicates what the code does.

Just compare

sort(files, less, &file_t::name);
accumulate(files, 0, plus, &file_t::size);

and

sort(files, projected_fn { less, &file::name })
accumulate(files, 0, composed_fn { plus, &file_t::size });

We could also create some cooler syntax like the pipe syntax for function transformation and have syntax like this:

sort(files, ascending | on_member(&file::name))

… but that is out of the scope of this post :)